Link
SimpleFOCDocs
Search

磁场定向控制算法简介 v2.0.2

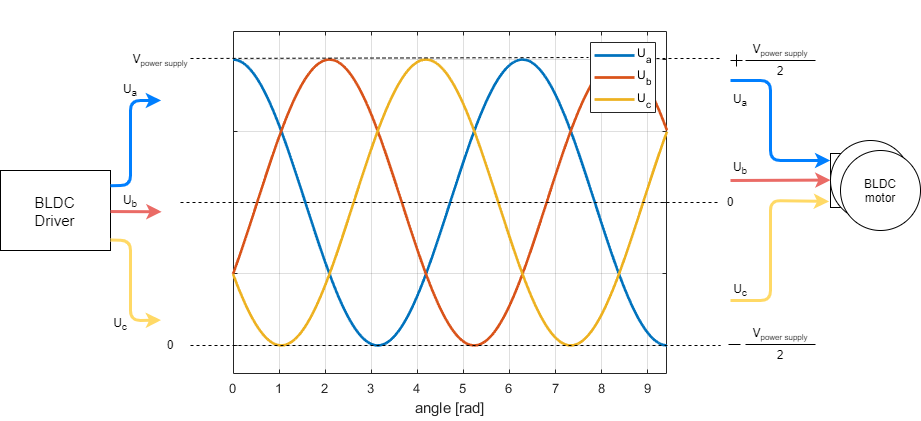
磁场定向控制算法的主要任务是接收用户定义的电压 uq，并通过持续读取电机转子位置 a，计算出合适的相电压 ua、ub 和 uc。

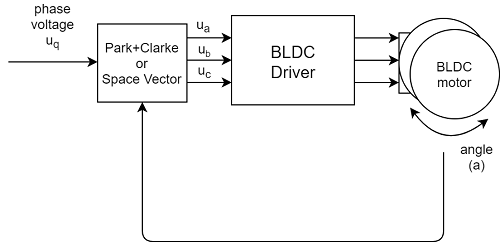
FOC 算法计算出的相电压会在电机定子中产生磁场，该磁场与转子永磁体的磁场恰好成 90 度“滞后”，从而产生推动效果。这里有一个非常棒的动画，展示了在运行名为六步调制的简化版 FOC 时，电机内部的情况。

via Gfycat

另一种理解为什么转子和定子磁场之间需要 90 度角的方式是，回忆一下通过磁场的导线所产生的电场力方程：

F = B*I*L*sin(alpha)

其中，B 是磁场强度，L 是导线长度，I 是电流大小，alpha 是磁场 B 和电流 I 之间的夹角。从这个方程可以看出，为了获得最大力 F = B*I*L，我们需要保持 alpha 角等于 90 度或 PI/2 弧度。

如何计算合适的电压 ua、ub 和 uc

由于 SimpleFOClibrary 旨在用于 FOC 算法的教学以及支持各种应用，该库中实现了两种最标准的 FOC 调制版本。

  • 正弦脉冲宽度调制：SinePWM
  • 空间矢量脉冲宽度调制：SpaceVectorPWM

你可以通过设置 motor.foc_modulation 变量来配置它们：

motor.foc_modulation = FOCModulationType::SinePWM; // default
// or
motor.foc_modulation = FOCModulationType::SpaceVectorPWM;

正弦调制 SinePWM

正弦调制基于两个变换方程。

逆帕克变换：

\[U_{\alpha} = U_q sin(\theta)\] \[U_{\beta} = U_q cos(\theta)\]

逆克拉克变换

\[u_a = U_{\alpha}\] \[u_b = \frac{-U_{\alpha} + \sqrt{3}U_{\beta}}{2}\] \[u_c = \frac{-U_{\alpha} - \sqrt{3}U_{\beta}}{2}\]

以下是SimpleFOC库中正弦脉冲宽度调制（Sinusoidal PWM）的实现代码：

// Method using FOC to set Uq to the motor at the optimal angle
void BLDCMotor::setPhaseVoltage(float Uq, float angle_el) {
    // Sinusoidal PWM modulation 
    // Inverse Park + Clarke transformation

    // angle normalization in between 0 and 2pi
    // only necessary if using _sin and _cos - approximation functions
    angle_el = normalizeAngle(angle_el + zero_electric_angle);
    // Inverse park transform
    Ualpha =  -_sin(angle_el) * Uq;  // -sin(angle) * Uq;
    Ubeta =  _cos(angle_el) * Uq;    //  cos(angle) * Uq;

    // Inverse Clarke transform
    Ua = Ualpha + voltage_power_supply/2;
    Ub = -0.5 * Ualpha  + _SQRT3_2 * Ubeta + voltage_power_supply/2;
    Uc = -0.5 * Ualpha - _SQRT3_2 * Ubeta + voltage_power_supply/2;

    // set the voltages in hardware
    setPwm(Ua, Ub, Uc);
}

空间矢量调制 SpaceVectorPWM

空间矢量调制基于两个计算步骤：

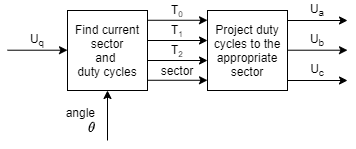
第一步，我们确定转子当前所在的扇区 s。360 度的角度被等分为 6 个 60 度的部分。所以这个计算非常直接。然后我们计算时间 T0、T1 和 T2。T1 和 T2 告诉我们相 1 和相 2 应该导通多长时间，T0 告诉我们电机应该有多长时间处于 0 电压状态。


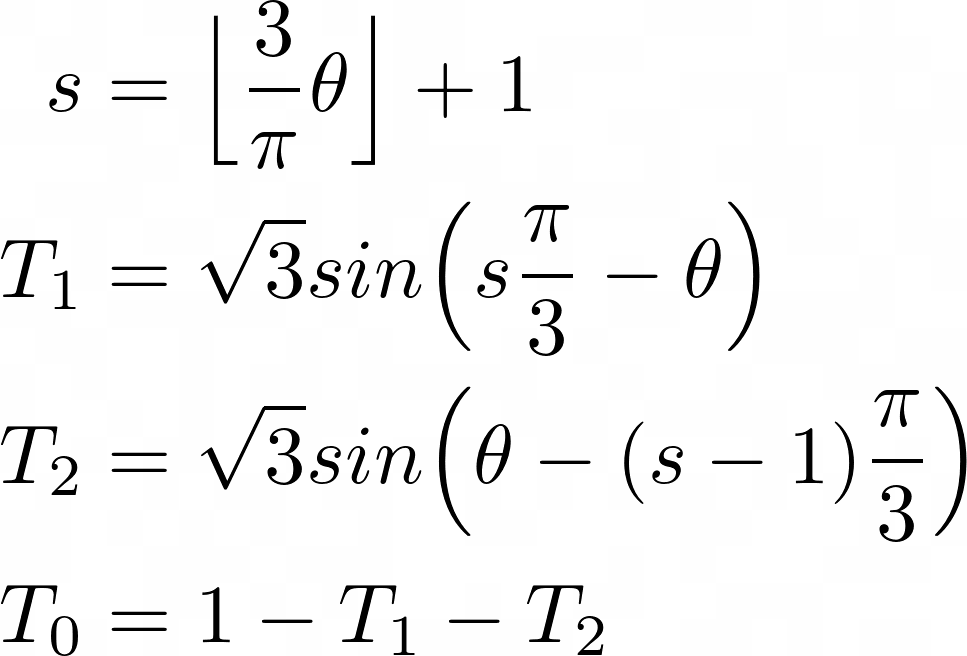
第二步是将 T0,1,2 值投影到适当的占空比 Ta,b,c，这直接取决于电机当前所在的扇区。

扇区TaTbTc
1T1 + T2 + T0/2T2 + T0/2T0/2
2T1 + T0/2T1 + T2 + T0/2T0/2
3T0/2T1 + T2 + T0/2T2 + T0/2
4T0/2T1+ T0/2T1 + T2 + T0/2
5T2 + T0/2T0/2T1 + T2 + T0/2
6T1 + T2 + T0/2T0/2T1 + T0/2

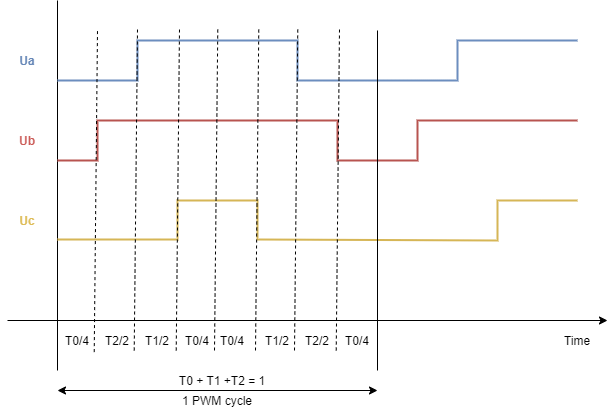
以下是使用 SVM 表为参数生成的 pwm 信号示例：s = 2，T1 = 1/8 = 0.125，T2 = 1/8 = 0.125 和 T0 = 1/2 = 0.5

以下是SimpleFOC库中空间矢量脉冲宽度调制（Space Vector PWM）的实现代码：

// Method using FOC to set Uq to the motor at the optimal angle
void BLDCMotor::setPhaseVoltage(float Uq, float angle_el) {
    // Nice video explaining the SpaceVectorModulation (SVPWM) algorithm 
    // https://www.youtube.com/watch?v=QMSWUMEAejg

    // if negative voltages change inverse the phase 
    // angle + 180degrees
    if(Uq < 0) angle_el += _PI;
    Uq = abs(Uq);

    // angle normalisation in between 0 and 2pi
    // only necessary if using _sin and _cos - approximation functions
    angle_el = normalizeAngle(angle_el + zero_electric_angle + _PI_2);

    // find the sector we are in currently
    int sector = floor(angle_el / _PI_3) + 1;
    // calculate the duty cycles
    float T1 = _SQRT3*_sin(sector*_PI_3 - angle_el) * Uq/voltage_power_supply;
    float T2 = _SQRT3*_sin(angle_el - (sector-1.0)*_PI_3) * Uq/voltage_power_supply;
    // two versions possible 
    // centered around voltage_power_supply/2
    float T0 = 1 - T1 - T2;
    // pulled to 0 - better for low power supply voltage
    //float T0 = 0;

    // calculate the duty cycles(times)
    float Ta,Tb,Tc; 
    switch(sector){
    case 1:
        Ta = T1 + T2 + T0/2;
        Tb = T2 + T0/2;
        Tc = T0/2;
        break;
    case 2:
        Ta = T1 +  T0/2;
        Tb = T1 + T2 + T0/2;
        Tc = T0/2;
        break;
    case 3:
        Ta = T0/2;
        Tb = T1 + T2 + T0/2;
        Tc = T2 + T0/2;
        break;
    case 4:
        Ta = T0/2;
        Tb = T1+ T0/2;
        Tc = T1 + T2 + T0/2;
        break;
    case 5:
        Ta = T2 + T0/2;
        Tb = T0/2;
        Tc = T1 + T2 + T0/2;
        break;
    case 6:
        Ta = T1 + T2 + T0/2;
        Tb = T0/2;
        Tc = T1 + T0/2;
        break;
    default:
        // possible error state
        Ta = 0;
        Tb = 0;
        Tc = 0;
    }

    // calculate the phase voltages
    Ua = Ta*voltage_power_supply;
    Ub = Tb*voltage_power_supply;
    Uc = Tc*voltage_power_supply;

    // set the voltages in hardware
    setPwm(Ua, Ub, Uc);
}

我应该使用哪一个？

以下是正弦调制和空间矢量调制在 Uq = 0.5V 时生成的波形图像。

正弦空间矢量

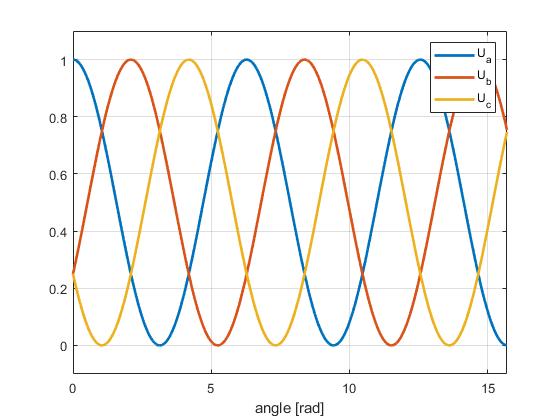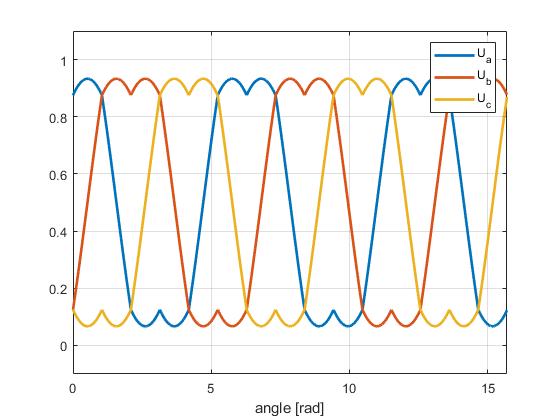这两种算法之间有几个关键区别。但就 SimpleFOClibrary 而言，你只需要知道空间矢量算法能更好地利用电源的最大电压范围。在上面的表格中，你可以看到对于 Uq = 0.5V，正弦调制生成的正弦波幅度恰好等于 1，而空间矢量调制还没有达到这个程度。空间矢量产生的“双正弦”波的幅度降低了 2/sqrt(3) = 1.15 倍，这意味着使用相同的电源，它可以向电机输送 15% 更多的功率。

这意味着，对于你的电源电压 Vpower_supply，当使用 SinePWM 时，你能够设置的最大 Uq = 0.5 Vpower_supply ，而如果使用 SpaceVectorPWM，你能够设置的最大 Uq = 0.58 Vpower_supply

电源电压 Vpower_supply 你应该通过更改参数 motor.voltage_power_supply 的值来指定。默认值设置为 12V。如果你将 Vpower_supply 设置为其他值，请在此处更改，以便 FOC 算法适应适当的 Uq（motor.voltage_q）值。

// power supply voltage
motor.voltage_power_supply = 12;

如果我不指定这个参数会怎样？

如果你不设置 motor.voltage_power_supply，算法仍然会工作，但你的 motor.voltage_q 值将不再等于实际输出电压。

当我超过最大 Uq 时会发生什么？

如果你尝试将电压 Uq 设置为高于 SinePWM 的 Uq = 0.5 Vpower_supply 或 SpaceVectorPWM 的 Uq = 0.58 Vpower_supply ，它仍然会工作，但 Ua,b,c 信号将会饱和。

以下是不同 Uq 值下 SinePWM 的几张图像。

Uq = 0.5 Vpower_supply Uq = 0.6 Vpower_supply Uq = Vpower_supply

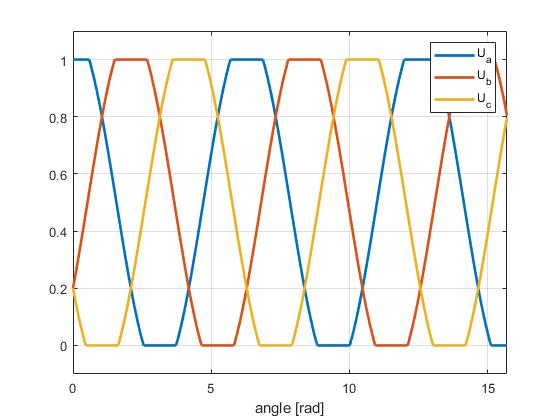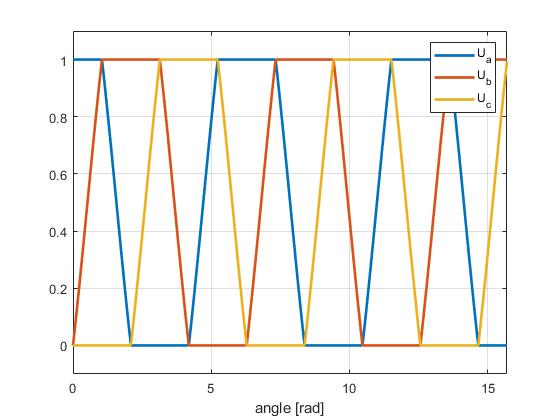基本上，你在图像上可以看到，Ua,b,c 已经饱和，并且在超过最大值后，你实际上不再向电机设置正弦波了。 电机仍然会获得一些功率增加，但不再是线性或平滑的。

经验法则

实际上，电机在 Uq ~ 0.7 Vpower_supply 之前都能察觉到差异。超过这个值后，Ua,b,c 过于饱和，进一步增加 Uq 不会导致电机功率增加。 但是每个电机都略有不同，你可以轻松地凭经验检查这些值。只需将电机置于电压控制下，观察在电压 Uq 的哪个值之后，你再也看不到电机功率的提升（它会停止加速）。

进一步阅读

有关初始化过程、实时执行和实现细节的更多信息，请访问 FOC 实现文档。