PID控制器原理 v2.1

本库实现的PID控制器的传递函数为：

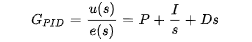
连续PID被转换到离散域，可以描述为三个部分的总和：

比例部分：

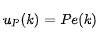
积分部分：

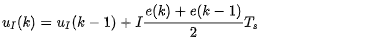
微分部分：

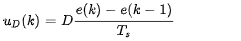
其中，u(k)是时刻k的控制信号（在我们的例子中是电压U_q），e(k)、e(k-1)是当前时刻k和前一步k-1的跟踪误差。跟踪误差是目标速度值v_d和测量速度v之间的差值。

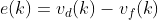
实现细节

PID算法在SimpleFOC库中通过PIDController类实现。实例化该类时需要指定参数。

PIDController(float P, float I, float D, float ramp, float limit);

该类只有一个函数：

// PID controller function
float PIDController::operator() (float error){
    // calculate the time from the last call
    unsigned long timestamp_now = _micros();
    float Ts = (timestamp_now - timestamp_prev) * 1e-6;
    // quick fix for strange cases (micros overflow)
    if(Ts <= 0 || Ts > 0.5) Ts = 1e-3; 

    // u(s) = (P + I/s + Ds)e(s)
    // Discrete implementations
    // proportional part 
    // u_p  = P *e(k)
    float proportional = P * error;
    // Tustin transform of the integral part
    // u_ik = u_ik_1  + I*Ts/2*(ek + ek_1)
    float integral = integral_prev + I*Ts*0.5*(error + error_prev);
    // antiwindup - limit the output voltage_q
    integral = _constrain(integral, -limit, limit);
    // Discrete derivation
    // u_dk = D(ek - ek_1)/Ts
    float derivative = D*(error - error_prev)/Ts;

    // sum all the components
    float output = proportional + integral + derivative;
    // antiwindup - limit the output variable
    output = _constrain(output, -limit, limit);

    // limit the acceleration by ramping the output
    float output_rate = (output - output_prev)/Ts;
    if (output_rate > output_ramp)
        output = output_prev + output_ramp*Ts;
    else if (output_rate < -output_ramp)
        output = output_prev - output_ramp*Ts;

    // saving for the next pass
    integral_prev = integral;
    output_prev = output;
    error_prev = error;
    timestamp_prev = timestamp_now;
    return output;
}

因此，你可以很容易地将PID集成到你的代码中。

void setup(){
  ...
  PIDController some_pid = PIDController{.....};
  ...
}
void loop(){
  float control = some_pid(target-measurement);
} 

这个PID类在BLDCMotor和StepperMotor类中实现，用于处理运动控制的速度（motor.PID_velocity）和位置（motor.P_angle）。你可以通过修改这些PID控制器的公共变量来改变它们的参数：

// PID controller configuration structure
class PIDController
{
  .....
  float P; //!< Proportional gain 
  float I; //!< Integral gain 
  float D; //!< Derivative gain 
  ....
};

例如:

motor.PID_velocity.P = 1;
motor.P_angle.P = 10;